Context Free Grammer

• Terminal Symbols = token
• Non-terminal Symbols = abstractions, inside of "< >"

In formal language theory, a context-free grammar (CFG) is a formal grammar whose production rules are of the form

A => a

• A: Non terminal

• a: terminals

• Abstraction: <assign> is a abstraction

• Production: <assign> -> <var> = <expression>

Example production:

<assignment> -> tID tASSGN tID; // For first assignment statement
<assignment> -> tID = tID + tID;       <-- Production 1
                | tId = tID;           <-- Production 2

But also we can write some type statement x = y + z * x So we should have write our production to handle more complex statements. So recursion can help us.

<assignment> -> tID = <expr>
<expr> -> tID              // Recursive role
        | <expr> + <expr>
        | <expr> * <expr>  

Derivations

• All CFG starts with start symbol
• Sentential form: A sentential form is any string derivable from the start symbol [wpi.edu]. applying productions to nonterminals in a sentential form. (recursively)
• Example: Let's take <program> a start symbol. Sentential forms can be :

begin <stmt_list> end                  OR
begin <stmt> ; <stmt_list> end

• We can generate multiple sentential forms of a program with openin productions which called as derivation.
• We use ==> to express derivation.

begin <stmt list> end ==> begin <stmt> ; <stmt list> end

Leftmost Derivation

• If we derive from left-hand side it will become leftmost derivation.
• Leftmost sentential form

<program> ==> begin <var> = <expr> end
          ==> begin tIDENT = <expr> end
          ==> begin tIDENT = <var> + <var> end
          ==> begin tIDENT = tIDENT + <var> end
         ......

Rightmost Derivation

• If we derive from right-hand side it will become rightmost derivation.
• Rightmost sentential form

<program> ==> begin <var> = <expr> end
          ==> begin <var> = <var> + <var> end
          ==> begin <var> = <var> + tIDENT end
          ==> begin <var> = tIDENT + tIDENT end
         ......

• When sentential form only have terminal it will become a sentence (program).

Parse Tree

• We can not see order of derivation in parse trees.

Hierarchy of syntactic structure of the sentence:

begin A = C + B end

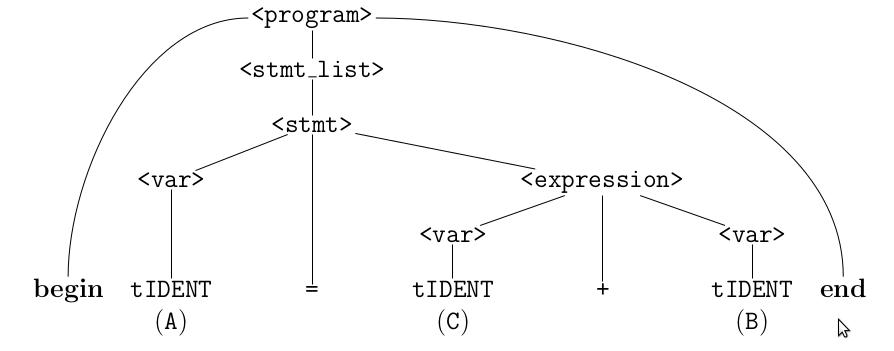
Yield: How parser read labels in this example (A - C - B)

Ambiguity

• We can have multiple parse tree for same program which we called as ambigious grammer. So we need some kind of priority operations.
• There are two source of ambigiouty
• Precende - Priority
• Associativty

A = B + C * A

<assign> -> tIDENT = <expr>
<expr>   -> <expr> + <expr>
          | <expr> * <expr>
          | tIDENT

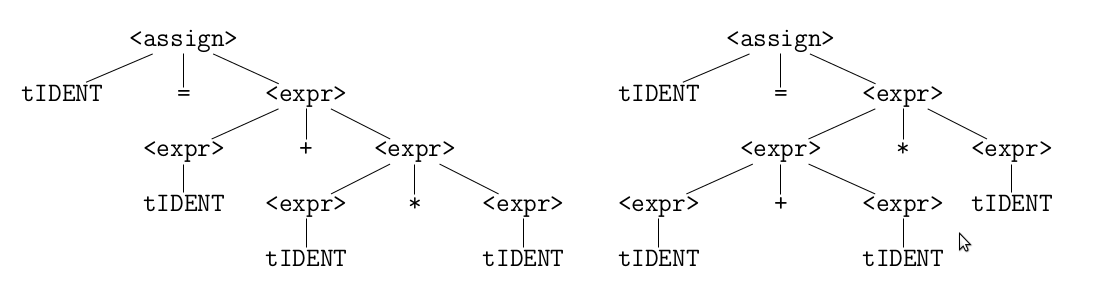
Operator precedence (öncelik)

• For example * has a higher priority than the + or -.

Operator Associativity

• A - B - C
• We need to know how to parse these values:
• (A-B) - C
• A - (B-C)

Left associative

• Example: (3-2) - 1 = 0

<assign> -> tID = <expr>
<expr> -> <expr> + <term> // Lowe priority root tree'ye yakın olan 
   |        |    | ==> left recursive rule left associativty
   ¯¯¯¯¯¯¯¯¯¯  
        | <term>

==> <term> + <term> ...

Right associative

• Example: 3- (2 - 1) = 2

<term> -> <term> * tID
        | tID

==> <tID> + <tID> ...

If statement ambigioty

This is dangling else problem. We don't know else is belong to which if statement.

Our grammer:

<if> -> if <bool> then <stats>
     |  if <bool> then <stats> else <stats>

<stats> -> <if> | <asgn> | <while> ....

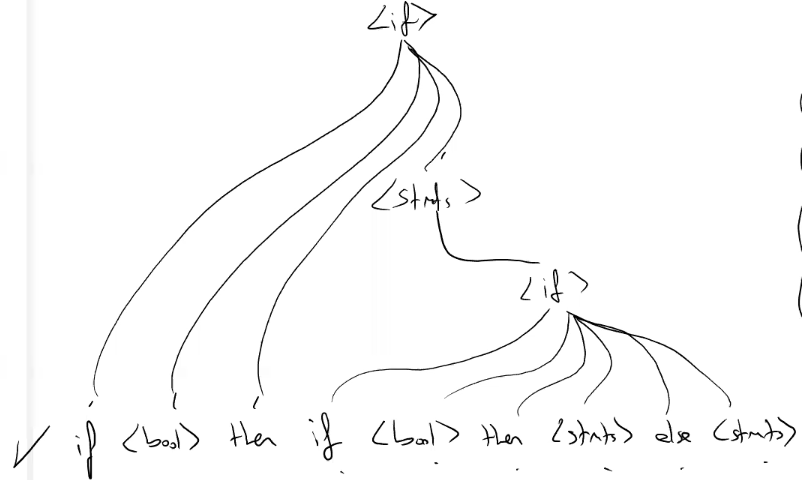
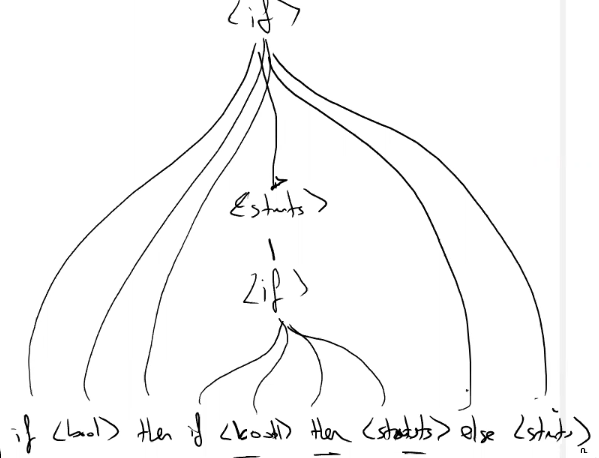
The solution: else is belong to nearest if statement. So we need to modify our grammer.

<unmatched> -> if <bool> then <stats>
<matched>   -> if <bool> then <matched> else <stats>
             | <assgn>
             | <for>

<stats> -> <matched> | <unmatched>

This was the end of the blog post. You can reach me via email umusasadik at gmail com